Самоучитель AutoCAD 3D
4.4. Типовые трехмерные тела (тела-примитивы)
Твердотельные объекты наиболее полно из всех типов трехмерных моделей отражают свои свойства, например, массу, объем и момент инерции.
В трехмерной графике AutoCAD существует некоторая группа объемных тел, называемых телами-примитивами, геометрическая форма которых уже заранее определена применением специальных инструментов моделирования.
В двухмерной графике геометрические примитивы – это отрезок, круг, прямоугольник, эллипс и т.д. В 3D такими примитивами являются тела: параллелепипед, шар, цилиндр, конус, клин, тор, пирамида и политело, техника работы с которыми и будет рассмотрена ниже.
Так для чего все-таки нужны объемные примитивы и какова область их практического применения в трехмерном моделировании? В некоторых случаях тела-примитивы могут быть использованы в следующих приложениях:
- В качестве вспомогательных тел для последующего объединения с базовым телом или вычитания их из него (операции с трехмерными объектами, о которых ниже будет подробно рассказано).
- В предварительных (черновых) компоновках сложных составных моделей в качестве опять-таки вспомогательных тел (тел замещения), которые впоследствии будут заменены детализированными оригиналами.
- Для предварительных оценок масс инерционных параметров будущего изделия или определения плотности его компоновки.
Способы доступа к инструментам:
- ГМн > Рисование > Моделирование > выбор пункта;
- Лента > Главная > Моделирование > выбор инструмента;
- Лента > Тело > Примитив > выбор инструмента.

Работа с инструментом Политело напоминает работу с инструментами плоского рисования Мультилиния и Полилиния, параметры которых задаются по приглашениям КС и вводятся с клавиатуры.
Для построения трехмерного примитива инструментом Политело первоначально необходимо задать определенные параметры. На рис. 4.5 показано несколько вариантов абстрактных фигур, созданных инструментом Политело.
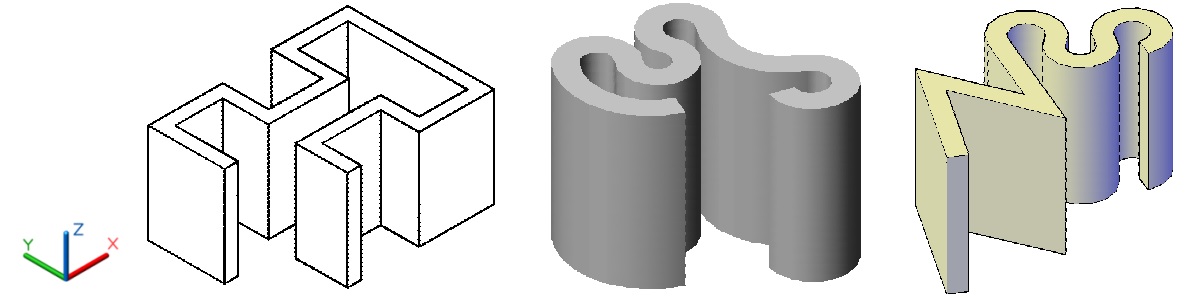
Рис. 4.5. Тела, созданные инструментом Политело
С помощью инструмента Ящик формируются твердотельные тела примитивы в виде куба или параллелепипеда, рис. 4.6.
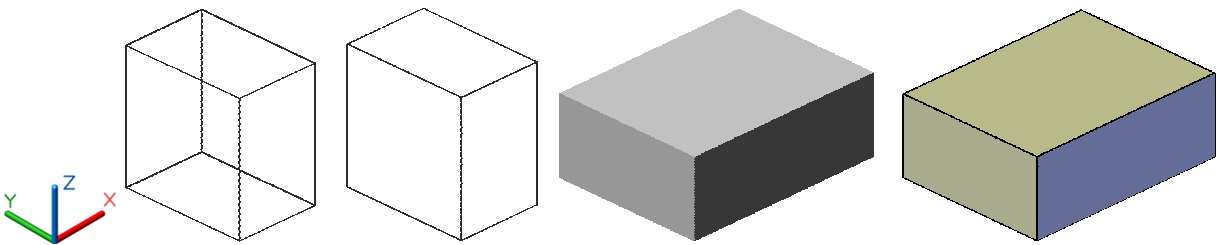
Рис. 4.6. Параллелепипеды в различных визуальных стилях
Активизируйте любым способом инструмент Ящик и по приглашениям КС выполните следующий алгоритм:
- Первый угол или [Центр]: указать ЛКн любую точку рабочего пространства;
- Другой угол или [Куб/Длина]: ПКн > КМн > выбрать пункт, например, Длина;
- Длина: ввести в КС численное значение ⇒ Ent;
- Ширина: ввести в КС численное значение ⇒ Ent;
- Высота или [2 точки]: ввести в КС численное значение ⇒ Ent.
Основание созданного параллелепипеда всегда параллельно плоскости XY текущей ПСК.

Инструментом Клин создается твердотельный объект, напоминающий по форме разрезанный наклонной плоскостью параллелепипед. Основанием клина служит геометрическая фигура в виде квадрата или прямоугольника, которая находится в плоскости параллельной плоскости XY текущей ПСК. Варианты клинообразных примитивов показаны на рис. 4.7.
При вводе параметров клинообразного объекта необходимо указать координаты первого угла его основания, тогда наклонная грань будет расположена напротив этого угла. Высота клина может иметь положительное или отрицательное значение.
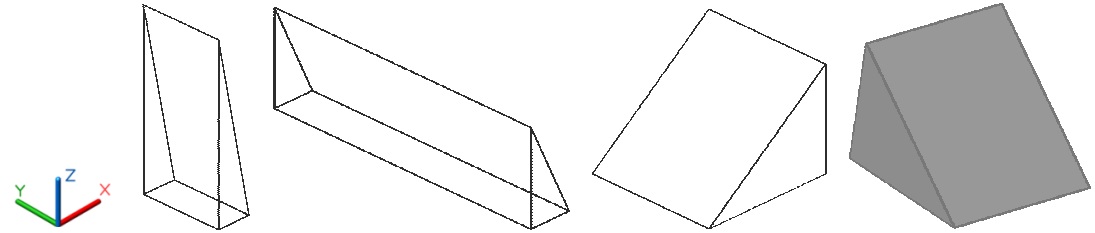
Рис. 4.7. Клинообразные тела в различных визуальных стилях
Активизируйте любым способом инструмент Клин и по приглашениям КС выполните алгоритм построения клина:
- Первый угол или [Центр]: указать щелчком ЛКн любую точку рабочего пространства;
- Другой угол [Куб/ Длина]: ПКн > КМн > выбрать пункт, например, Длина;
- Длина: ввести в КС численное значение ⇒ Ent;
- Ширина: ввести в КС численное значение ⇒ Ent;
- Высота или [2 т]: ввести в КС численное значение ⇒ Ent.
Если в КМн выбрать пункт Куб, то в приглашении КС появится только один запрос о высоте клина.

С помощью инструмента Конус в пространстве создаются примитивные тела конической формы, в том числе усеченные. Основанию конуса можно изначально задать геометрическую форму в виде круга или эллипса. На рис. 4.8 показаны конические тела, имеющие разные свойства: плотность каркаса, ориентацию в пространстве и визуальные стили отображения.
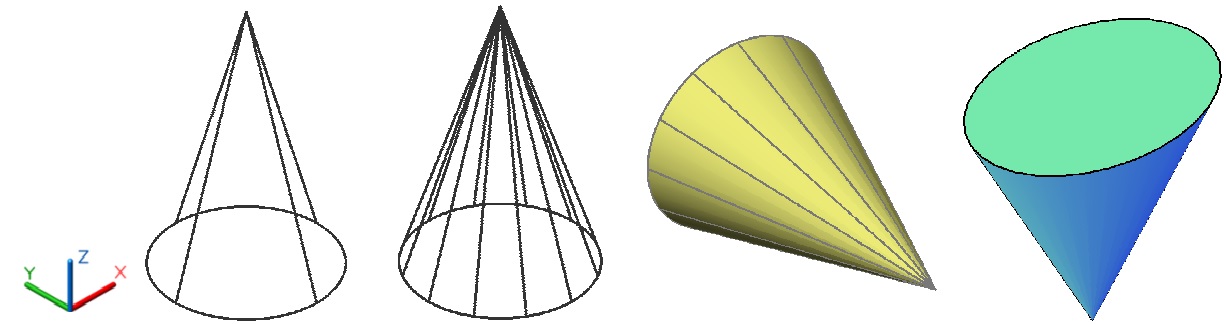
Рис. 4.8. Круглые и эллиптический (справа) конусы
Активизируйте любым способом инструмент Конус и по приглашениям КС выполните алгоритм:
- Центр основания или [3т/2т/Касательная/ Эллиптический]: щелкнуть ЛКн в любую точку рабочего пространства;
- Радиус основания цилиндра или [Диаметр]: ПКн > КМн > указать пункт Диаметр;
- Диаметр: ввести в КС численное значение ⇒ Ent;
- Высота или [2т/ Конечная точка оси/Верхний радиус]: ввести в КС численное значение ⇒ Ent.
На последнем шаге алгоритма построения конуса указано отрицательное значение его высоты, поэтому объект получился перевернутым.
Основание конуса всегда расположено в плоскости XY текущей ПСК, а вот если задать координаты вершины конуса, то его тело будет наклонено к плоскости XY.

Инструмент Сфера формирует в пространстве твердотельный объект в виде шара. На рис. 4.9, шары показаны в различных визуальных стилях отображения.
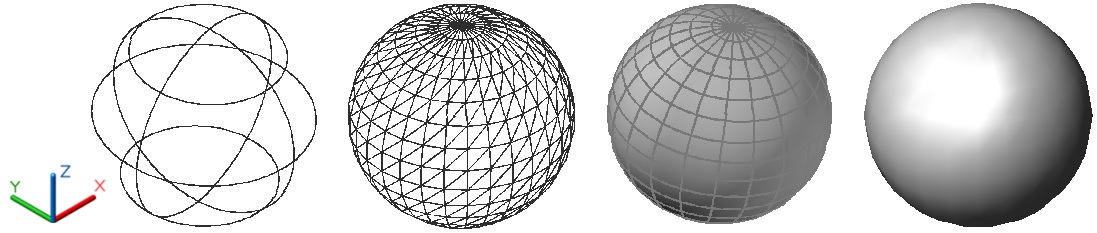
Рис. 4.9. Твердотельный шар
Активизируйте любым способом инструмент Сфера и по приглашениям КС выполните следующий алгоритм:
- Центр или [3т/2т/ККР]: указать ЛКн в любую точку рабочего пространства;
- Радиус или [Диаметр]: ПКн > КМн > указать пункт Диаметр;
- Диаметр: ввести в КС численное значение ⇒ Ent;
Шар самый простой по выполнению объемный примитив из существующих тел-примитивов в программе. При вводе параметров шара нужно задать только центральную точку и радиус (диаметр), причем центральная точка шара является его центром по всем трем осям.
Плотностью изолиний на поверхности объекта управляет системная переменная ISOLINES, значение по умолчанию которой равно 4.
Системная переменная ISOLINES определяет количество линий контура для изображения поверхностей сферических, цилиндрических, а также конических тел и может принимать значения: целые числа от 0 до 2047.
Чтобы визуально оценить полученные результаты необходимо после изменения значения переменной выполнить дополнительно регенерацию рисунка. Введите в КС команду регенерации: _REGEN Þ Ent. Регенерировать рисунок можно и другим способом:
Вид > выбрать пункт Регенерировать.
В некоторых случаях можно обновить и плоский рисунок. Вероятно, вы обращали внимание на то, что особенно при сочетании больших и малых форм в рисунке, круги становятся шестигранниками, а кривые – ломаными отрезками и вообще над рисунком довлеет квадратура круга? Если это вас раздражает, попробуйте выполнить регенерацию рисунка.

Инструмент Цилиндр позволяет сформировать твердотельное цилиндрическое тело с основанием в виде круга или эллипса, параллельного плоскости XY текущей ПСК, рис. 4.10.
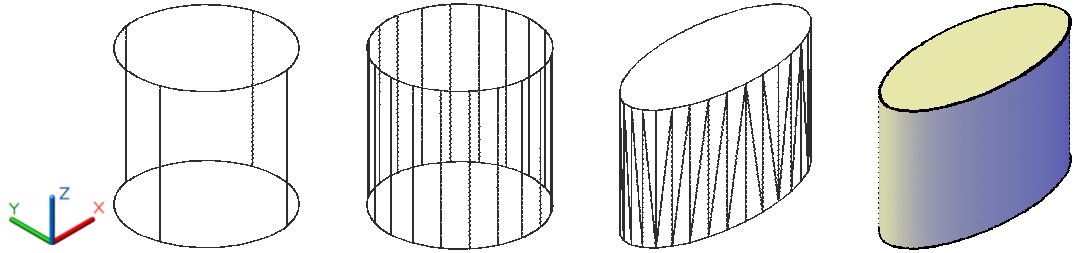
Рис. 4.10. Цилиндры круглой и эллиптической формы
Активизируйте любым способом инструмент Цилиндр и по приглашениям КС выполните следующий алгоритм:
- Центр основания или [3т/2т/ККР /Эллиптический]: щелкнуть ЛКн в любую точку пространства;
- Радиус основания или [Диаметр]: ПКн > КМн > выбрать пункт Диаметр;
- Диаметр: ввести в КС численное значение ⇒ Ent;
- Высота или [2т/Конечная точка оси]: ввести в КС численное значение ⇒ Ent.
Возможно построение цилиндрического тела с эллиптическим основанием, если в первом пункте алгоритма щелкнуть ПКн и выбрать пункт Эллиптический.

Для построения твердотельного тора необходимо задать всего лишь два параметра – это непосредственно диаметр тора и диаметр его полости. Под полостью подразумевается в данном случае его твердотельная часть.
Что бы получился полноценный тор (с центральным отверстием) необходимо выполнить одно условие: диаметр тора должен быть всегда больше чем диаметр его полости. Варианты визуализации тора показаны на рис. 4.11.

Рис. 4.11. Варианты визуализации тора
Если это условие выполнить наоборот, то в результате получится так называемый самопересекающийся тор, т.е. тор у которого отсутствует центральное отверстие.
Активизируйте любым способом инструмент Тор и по приглашениям КС выполните следующий алгоритм:
- Центр или [3т/2т/ККР]: указать щелчком ЛКн любую точку рабочего пространства;
- Радиус или [Диаметр]: ПКн < КМн > выбрать пункт Диаметр;
- Диаметр: ввести в КС численное значение ⇒ Ent;
- Радиус полости или [2 т/Диаметр]: ввести в КС численное значение ⇒ Ent.
По аналогии с построением шара, плоскость XY делит твердотельный тор на две равные части в продольном сечении.

Основанием пирамиды служит плоская геометрическая фигура с числом сторон то 3-х до 32-х, лежащая в плоскости параллельной плоскости XY текущей ПСК, рис. 4.12. Вершиной пирамиды может быть либо точка, либо многоугольник и если выбирается последний, то пирамида формируется усеченной.
Пирамиду также можно построить наклонной относительно плоскости XY, если выбрать из КМн опцию Конечная точка оси.
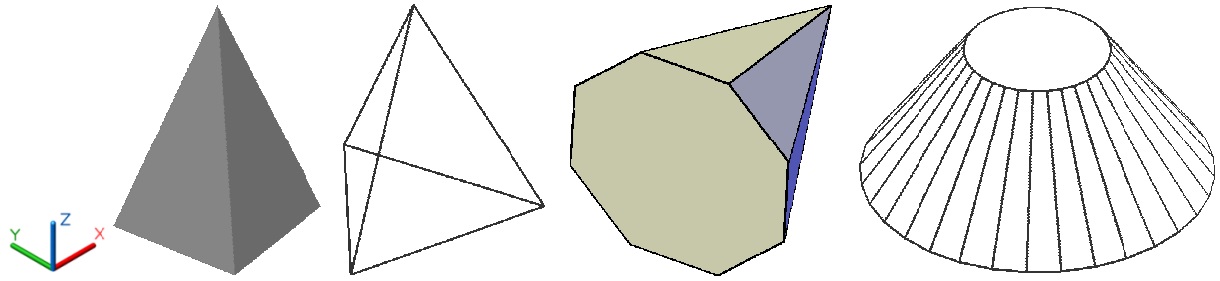
Рис. 4.12. Некоторые типы многоугольных пирамид
Активизируйте любым способом инструмент Пирамида и по приглашениям КС выполните алгоритм построения пирамиды:
- Центральная точка основания или [Кромка/Стороны]: щелкнуть ЛКн в любую точку рабочего пространства;
- Радиус основания или [Вписанный]: ввести в КС численное значение ⇒ Ent;
- Высота или [2 т/Конечная точка оси/Радиус верхнего основания]: ввести в КС численное значение ⇒ Ent.
Если вначале выполнения алгоритма щелкнуть ПКн и выбрать пункт Сторона, то в КС появится запрос: Число сторон <4>), в ответ на который необходимо ввести численный параметр многоугольника, служащего основанием пирамиды.
